|
|
Optimalna osnova brojevnog sistema za maĊĦinsko predstavljanje
Sa aspekta mašinskog predstavljanja važno je odrediti takvu osnovu brojevnog sistema (N),koja će obezbediti što manje različitih cifara (N) i što kraće zapise brojeva. Količina fizičkih elemenata u mašini (M) proporcionalna je broju različitih cifara (N) i dužini zapisa (n) : M=knN k- koeficijent proporcionalnosti
Zahtev za malim brojem različitih cifara i kratkim zapisom brojeva pomoću tih cifara uzajamno se isključuju. U sistemu sa osnovom N,maksimalan mogući n-tocifreni broj koji se u osnovi možezapisati je 
pa je za N>1 i dovoljno veliko n može se uzeti 
pa je 
zamenom u M=knN, dobija se
Sredimo N,Tako da broj mašinskih elemenata M bude minimalan. Mmin se dobija pod uslovom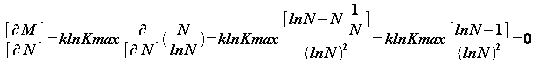 
odavde je lnN=1 => N=e=2.71...Teorijski optimalna osnova brojnog sistema koja za predstavljanje n-to cifrenih brojeva zahteva najmanje mašinskih elmenata iznosi e. S obzirom da osnova brojnog sistema mora biti ceo broj ostaje da se izabere 2 ili 3. Osnova 3 je bliža optimalnosti,ali se fizički element sa dva stanja prostije realizuje od onih sa tri stanja .To je razlog što se u praksi za predstavljanje brojeva koristi binarni sistem.