|
|
Metoda sukcesivnih eliminacija-odredjivanje opšteg rešenja Bulove jednačine
Bulova jednačina A(x1,...,xn)=B(x1,...,xn) transformiše se u ekvivalentnu 
koja ima oblik f(x1,...,xn)=0 Ovu jednačinu transformišemo u ekvivalentnu oblika: 
Ona je moguća akko f1(1,x2,...,xn)•f1(0,x2,...,xn)=0 Leva strana poslednje jednačine ima oblik f2(x2,...,xn)=0, gde je eliminisano x1. Sada sve ponavljamo za f2(x2,...,xn) i eliminišemo x2. Postupak eliminacije produžavamo do 
gde su fn(1)=a , fn(0)=b iz L2 tj do svodjenja na jednačinu sa jednom promenljivom. Ona je moguća akko ab=0 i njeno rešenje je: 
tj.
,gde je pn parametar iz L2. Zamenom xn u
odredjujemo 
, gde su pn-1 , pn parametri iz L2 . Na kraju se odredjuje 
, gde su p1,...,pn parametri iz L2. Zato je rešenje date jednačine odredjeno izrazima:
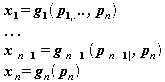
Vezu partikularnih rešenja sa opštim rešenjem Bulove jednačine da je terema Lowenheim-a :
Ako je 
partikularno re[enje jedna;ine f(x1,...,xn)=0 , onda je njeno opšte rešenje : 
,i=1,...,n , gde je p=(p1,...,pn) proizvoljan vektor iz 
.