|
|
|
Tjuringove mašine
Tjuringova mašina je teorijska konstrukcija namenjena ispitivanju svojstava algoritma. Od elektronskih računara razlikuje se pre svega, po elementarnosti algoritamskih koraka koji su maksimalno jednostavni. Na taj način logička struktura postupka poprima vrlo prost standardni oblik, pogodan za teorijsko istraživanje.
Mašina se sastoji od sledećih delova:
• Neograničena (potencijalno beskonačna) traka izdeljena na polja koja služi kao spoljašnja memorija,
• Glava za čitanje simbola iz polja trake i zapisivanje simbola u polja trake,
• Logički blok,
• Blok upravljanja.
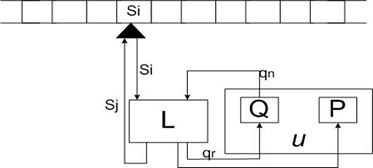
Tjuringova mašina radi u taktovima,što obezbedjuje blok za upravljanje U. Mašina raspolaže konačnim brojem simbola s1,s2,...,sk koji čine spoljni alfabet. Način prerade informacija odredjuje se u logičkom bloku L. Logički blok se može nalaziti u jednom od konačnog broja stanja.: q1,q2,...,qn.
Rad logičkog bloka u svakom taktu odvija se na sledeći način:
Po ulaznom kanalu iz glave za čitanje prima se simbol si, koji je glava pročitala sa trake. Drugi ulazni kanal u L donosi simbol stanja qn koje se bloku L propisuje za sledeći takt. Jednim izlaznim kanalom logički blok šalje “preradjeni” simbol sj koji se pomoću glave upisuje u polje nad glavom.Simbol sj jednoznačno je odrdjen ulaznim parom(si,qn). Drugim izlaznim kanalom logički blok šalje simbol stanja qr u blok upravljanja U, koji se u polju Q čuva do sledećeg takta. Trećim izlaznim kanalom iz L šalje se simbol pokretanja trake u polje P bloka upravljanja.Ovaj simbol obezbedjuje da se traka pomeri za jedno polje levo(L),desno(D) ili da se ne pomeri(N).Simbol pokretanja trake čuva se u polju P bloka upravljanja U do početka sledećeg takta. Blok upravljanja obezbedjuje da se na početku sledećeg takta simbol simbol qr vrati po liniji povratne veze u logički blok L,a znak pomak trake iz polja P pošalje u mehanizam koji vrši pomeranje trake.
Simboli stanja q1,...,qm i pomaka L,D,N sačinjavaju unutrašnji alfabet mašine. Važno je uočiti da u svakom taktu izlazna trojka simbola sj,P,qr , gde P∊{L,D,N}, jednoznačno zavisi samo od ulaznog para si,qn(takvih parova ima k x m) pridružuje trojku sj,P,qr. Ovu logičku funkciju mašine zgodno je prikazati tablicom koja se zove funkcionalna shema mašine. Funkcionalna shema je jedan standardni način zadavanja algoritma. Funkcionalna shema se može zadati i u obliku niza naredbi tipa: sq → s'Pq' koje se izvršavaju ovako: ako se u datom taktu čita simbol s u stanju q, onda se s zamenjuje sa s' , a u početku sledećeg takta izvršiće se pomeranje trake P(P je L,D,N) i u stanju q' čitaće se simbol iz vidnog polja trake. Takav niz naredbi zove se Tjuringov program. Rad Tjuringove mašine potpuno je dredjen zadavanjem njene funkcionalne sheme ili zadavanjem Tjuringovog programa.